
안녕하세요. 수이남입니다.
오늘은 수학 2의 세 번째 이야기 미분계수와 도함수입니다.
나중에 미분을 하기 위한 기초가 되니
충분히 학습해 두셔야 나중에
미분에서 어려움 없이 진도를 나갈 수 있습니다.
그럼 시작하겠습니다.
첫 번째, 미분계수
미분계수를 말하기 전에
변화율에 대해서 먼저 알아볼게요.
첫 번째, 평균 변화율
변화율이라는 것은 말 그대로
얼마큼 변화하는지 비율로 나타낸 것인데요.
그럼 미분에서 사용될 평균 변화율에 대해서
알아보겠습니다.
우선 평균 변화율을 정의하기 전에
"증분"이라는 단어부터 정의할게요.
증분이라는 것은
어떠한 값의 변화량을 의미합니다.
즉 x의 변화량은 x의 증분,
y의 변화량은 y의 증분이라고 하죠.
이 증분은 기호로 delta(Δ)를 사용하는데
보통 어떠한 값의 차를 말할 때 많이 사용되는 기호예요.
그래프로 본다면 아래와 같습니다.

정리해 보자면
x의 증분 : Δx = b - a
y의 증분 : Δy = f(b) - f(a)
입니다.
그럼 이제 증분을 알았으니,
평균 변화율에 대한 정의를 살펴볼게요.
평균 변화율이란
x의 증분에 대한 y의 증분의 비율입니다.
즉,

이렇게 표현할 수 있습니다.
또한 평균 변화율의 정의가
x의 증분에 대한 y의 증분의 비율인데,
이것은 일차함수에서 본 적이 있을 겁니다.
바로 일차함수의 기울기를 의미합니다!
그럼 평균 변화율은 다른 말로
(a, f(a))와 (b, f(b))를 지나는 직선의 기울기라고도
말할 수 있습니다.
위에서 b=a+Δx로 표현한 것은
b라는 점을 a에서 Δx만큼 더 간 점이라고 표현한 것입니다.
두 번째, 미분계수
그럼 이제 평균 변화율이라는 것이
무엇인지 알았으니
미분계수에 대해서 알아보겠습니다.
위에서 설명한 평균 변화율의 정의에서
Δx를 0에 한없이 가깝게 보낼 때,
y=f(x)의 극한값이 존재한다면 x=a에서 "미분 가능"하다고 합니다.
이때 극한값을 함수 y=f(x)의 x=a에서 순간 변화율 또는 미분계수라고 합니다.
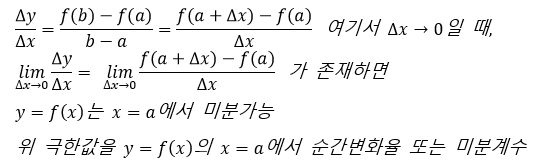
수식으로 정리하면 위와 같습니다.
그리고 y=f(x)는 x=a에서 미분계수는
f'(a)라고도 적을 수 있으며
f prime a라고 읽습니다.
정리하자면 아래와 같습니다.

세 번째, 미분계수의 기하적 의미
위의 미분계수를 수식으로는 굉장히
복잡해 보일 수 있지만
그래프로 표현해보면 간단합니다.
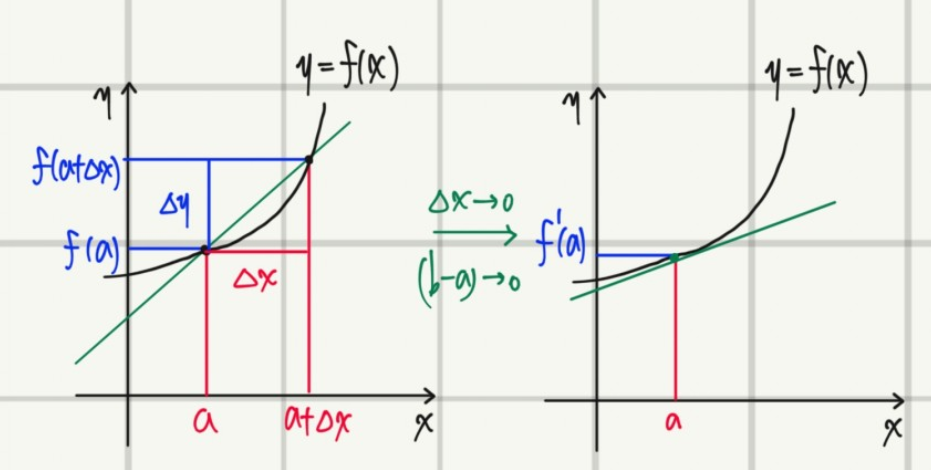
위와 같이 그래프로 나타낼 수 있으며
쉽게 말해
함수 f(x)의 x=a에서 미분계수 f'(a)는 곡선 y=f(x) 위의 점 (a, f(a))에서
접하는 접선의 기울기를 의미합니다.
네 번째, 미분가능성과 연속성
미분가능성과 연속성의 관계를 결론부터 말하자면
함수 f(x)가 x=a에서 미분 가능하면 f(x)는 x=a에서 연속입니다.
왜 이런 결과가 나왔는지
간단한 증명과정을 통해 알아보겠습니다.

극한의 성질을 이용하여 위와 같이 증명할 수 있습니다.
굳이 증명과정은 기억할 필요는 없고,
한번 따라 해 보시고
어떠한 함수가 미분 가능하면 연속이다!
라고만 정리 해 두시면 될 것 같습니다.
두 번째, 도함수
첫 번째, 도함수란?
자, 앞서 미분계수에 대해서 배워보았습니다.
미분계수란 어떠한 함수 y=f(x)에 대해서
x=a에서 미분 가능하다면
f'(a)를 미분계수라고 정의했습니다.
그럼 이 미분계수가 함수처럼 나타나 있다면?
그것을 바로 도함수라고 합니다.
즉, 미분계수와 도함수의 차이는
함수의 형태를 하고 있느냐 없느냐의 차이입니다.
개념적으로는 동일하다고 생각하셔도 괜찮습니다.
조금 더 수학적으로 설명드리자면
함수 f(x)가 정의역 X에서 미분 가능할 때,
정의역의 각 원소 x에 미분계수 f'(x)를 대응시키는
새로운 함수를 뜻합니다.
이때, f'(x)를 함수 f(x)의 도함수라고 합니다.
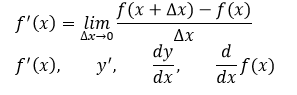
기호로는 위와 같이 표현할 수 있는데
dy/dx는 y를 x에 대하여 미분하라 라는 기호입니다.
무슨 말인지 이해하기 어려우실 거라고 생각됩니다..
쉽게 말해 f(x)에서 x의 임의의 값에 대해 미분 가능한데,
그 x의 값에 대해 대응되는 미분 값을
모아둔 함수라고 생각하시면 되겠습니다.
위의 도함수의 정의에서 Δx를 h로 쓰기도 합니다.
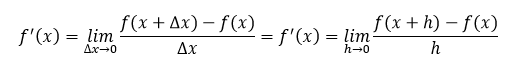
두 번째, 도함수를 구하는 방법
도함수를 구하는 방법은 증명과정보다는
결과가 너무 중요하기 때문에
결과만 보고 넘어가겠습니다.

위의 결과를 잘 정리해 두시기 바랍니다.
앞으로 다양한 함수들의 도함수를 배워나갈 예정입니다.
세 번째, 함수의 실수 배, 합, 차, 곱의 미분
함수의 실수 배에 대한 미분법입니다.

함수의 합과 차에 대한 미분법입니다.

함수의 곱에 대한 미분법입니다.

정리해보자면
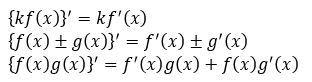
오늘 수학 2의 세 번째 이야기
미분계수와 도함수입니다.
중요한 부분이니
잘 정리하시면 좋겠습니다.
긴 글 읽어 주셔서 감사합니다.
'수학 이야기 > 수학2' 카테고리의 다른 글
| [여섯 번째 이야기]적분 - 부정적분과 정적분 (0) | 2020.08.08 |
|---|---|
| [다섯 번째 이야기]미분 - 도함수의 활용(2) (0) | 2020.08.07 |
| [네 번째 이야기] 미분 - 도함수의 활용(1) (3) | 2020.04.16 |
| [두 번째 수학이야기] 함수의 극한과 연속 - 함수의 연속 (0) | 2020.03.30 |
| [첫 번째 수학이야기] 함수의 극한과 연속 - 함수의 극한 (1) | 2020.03.25 |


