
안녕하세요. 수이남입니다.
오늘은 미적분의 네 번째 이야기
여러 가지 함수의 미분 두 번째입니다.
앞에서 삼각함수까지 다루기에는
글이 너무 길어질 것 같아
두 번에 걸쳐 여러 가지 함수의 미분에 대해서
적는 점 양해 부탁드립니다.
그럼 바로 시작하겠습니다.
세 번째, 삼각함수의 덧셈 정리
우선 삼각함수란 어떤 것인지
다들 잘 알고 계실 거라 생각합니다.
아직 제가 삼각함수에 대해서 정리해둔 글이 없어서
최대한 빠른 시간 내에 삼각함수도 정리할 수 있게
노력하겠습니다.
간단하게 소개하자면
삼각함수는 sin x, cos x, tan x, csc x, sec x, cot x 등이 있죠?
이러한 삼각함수에 대한 덧셈 정리를
정리해 보도록 할게요.
삼각함수의 덧셈 정리는 결과만 간단하게
살펴보고 넘어가겠습니다.
증명과정이 복잡한 것은 아닌데,
증명과정에서 수학적으로 눈여겨 볼만한 과정도 아니고
결과만 잘 적용한다면 크게 상관이 없는 부분이라
덧셈 정리에 대한 결과만 살펴보겠습니다.
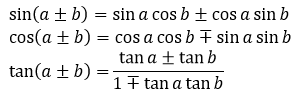
흔히들 앞글자만 따서 많이 외우시더라고요.
어떠한 방식으로든 위의 덧셈 정리를 외워두셔야 합니다.
네 번째, 삼각함수의 극한
이번엔 삼각함수의 극한에 대해서
알아보겠습니다.
첫 번째, 삼각함수의 극한
삼각함수의 극한도 앞서
지수함수와 로그함수의 극한값을 구한 것처럼
구하면 됩니다.
간단하게 sin x, cos x, tan x만 살펴보겠습니다.

그래프로 보면 위와 같습니다.
삼각함수 중 sin과 cos 함수는
어떤 임의의 실수 a에 대해서 극한값을 가집니다.
하지만 양의 무한대와 음의 무한대의 극한값은
존재하지 않습니다.
sin과 cos은 주기 함수로서 계속해서 진동하기 때문입니다.
그리고 tan함수는 임의의 실수 b에 대해서
극한값을 가집니다.
하지만 b는 nπ/2에 대해서는 연속하지 못하므로
극한값을 가질 수 없습니다.
(여기서 n은 음 또는 양의 자연수 입니다.)
즉, 한 개의 주기로만 본다면
-π/2와 π/2에서는
연속하지 못하므로 극한값이 존재하지 않습니다.
tan함수 또한 양의 무한대와 음의 무한대에 대해서
주기 함수를 나타내므로 극한값은 존재하지 않습니다.
수식으로 정리해보자면
아래와 같습니다.

아래의 극한값은 존재하지 않습니다.

위는 일반적인 삼각함수에 대한 극한값을 알아보았습니다.
그렇다면
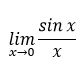
오른쪽의 극한값은
어떻게 구할 수 있을까요?

첫 번째, 0 < x < π/2 일 때
위의 그림에서
반지름이 1인 원 O에서
∠AOB의 크기를 x 라디안이라고 하고,
점 A에서 접하는 접선과 선분 OB의 연장선의 교점을 T라고 하면
△AOB의 넓이 < 부채꼴 AOB의 넓이 < △AOT의 넓이입니다.
그럼 삼각형과 부채꼴의 넓이 공식을 이용하여 표현한다면
1/2 * sin x < 1/2 x < 1/2 * tan x입니다.

위 사진은 삼각형과 부채꼴의 넓이 공식입니다.
수학 1에서 나오는 내용입니다.
1/2 * sin x < 1/2 x < 1/2 * tan x 이 식을 정리하면
sin x < x < tan x이고
sin x > 0 이므로 각 변을 sin x로 나누면
부등호의 방향은 변하지 않고
1 < x / sin x < tan x / sin x이고,
tan x / sin x = 1 / cos x 이므로
1 < x / sin x < 1 / cos x입니다.
각 항을 역수를 취하면
부등호의 방향이 바뀌고
cos x < sin x / x < 1입니다.
그리고 각 항을 0+에 극한을 취하면 아래와 같습니다.

그리고 샌드위치 정리에 의해서

이 됩니다.
샌드위치 정리에 관한 글은 밑에 링크 참고바랍니다.
https://mathmen.tistory.com/10
-π/2 < x < 0에 대해서 x = -t로 치환한다면
x -> 0+ 이 t -> 0- 이므로
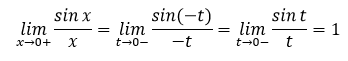
위의 결과가 나옵니다.
그럼 최종적으로
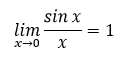
이 됩니다.
여기서 x는 라디안을 사용했다는 것을
주의해 주세요.
다섯 번째, 삼각함수의 미분
이제는 본격적으로
삼각함수의 미분에 대해서 알아보겠습니다.
오늘은 sin x와 cos x의 도함수에 대해서 알아보겠습니다.
결과부터 본다면

입니다.
이것 또한 도함수의 정의를 이용하여 증명해본다면
아래와 같습니다.
(증명과정은 넘어가셔도 괜찮습니다.
위의 결과만 정확히 알고 계시면 됩니다.)

오늘 여러 가지 함수의 미분법(2)은 여기까지입니다.
미분과 적분은 나중에도 정말 많이 이용되니
배우실 때 확실히 이해하시고 넘어가셨으면
좋겠습니다.
오늘도 긴 글 읽어 주셔서 감사합니다.
'수학 이야기 > 미적분' 카테고리의 다른 글
| [여섯 번째 이야기]미분법 - 여러 가지 미분법(2) (0) | 2020.08.08 |
|---|---|
| [다섯 번째 이야기]미분법 - 여러 가지 미분법(1) (0) | 2020.08.08 |
| [세 번째 이야기] 미분법 - 여러 가지 함수의 미분(1) (0) | 2020.04.08 |
| [두 번째 이야기] 수열의 극한 - 급수 (0) | 2020.04.01 |
| [첫 번째 이야기] 수열의 극한 - 수열의 극한 (0) | 2020.03.27 |

